凸包
计算几何的一大重要内容
维护凸壳
这个我喜欢读(tu1 ke2)。我们先从简单的入手。
这个分为上凸壳和下凸壳。顾名思义就是一个维护多条函数的最大值,一个维护最小值。
这个我们有一个例题 水平可见直线
其实是因为考场上没学但是写出来了而作为纪念找到的!(虽然那道题还是因为没调完爆零了/kk)
我们考虑按照每条直线的斜率排序,然后就可以得到非常不错的结果。因为斜率最大的和斜率最小的代表了两边界,可以很顺利的一路搭过来。
其中我们用单调栈来维护这些线段。一般我们考虑栈中的后两个直线以及当前的直线。很显然,因为当前的直线是目前所有直线中斜率最小的,所以它一定在某一处可以成为最大值,具体的位置是相对靠近左的。所以我们考虑新加进来的直线对之前栈中其他直线的影响。
还是得要一张图,这张图讲得还是挺详细的,就不多说了,直接看图也就差不多能懂了。
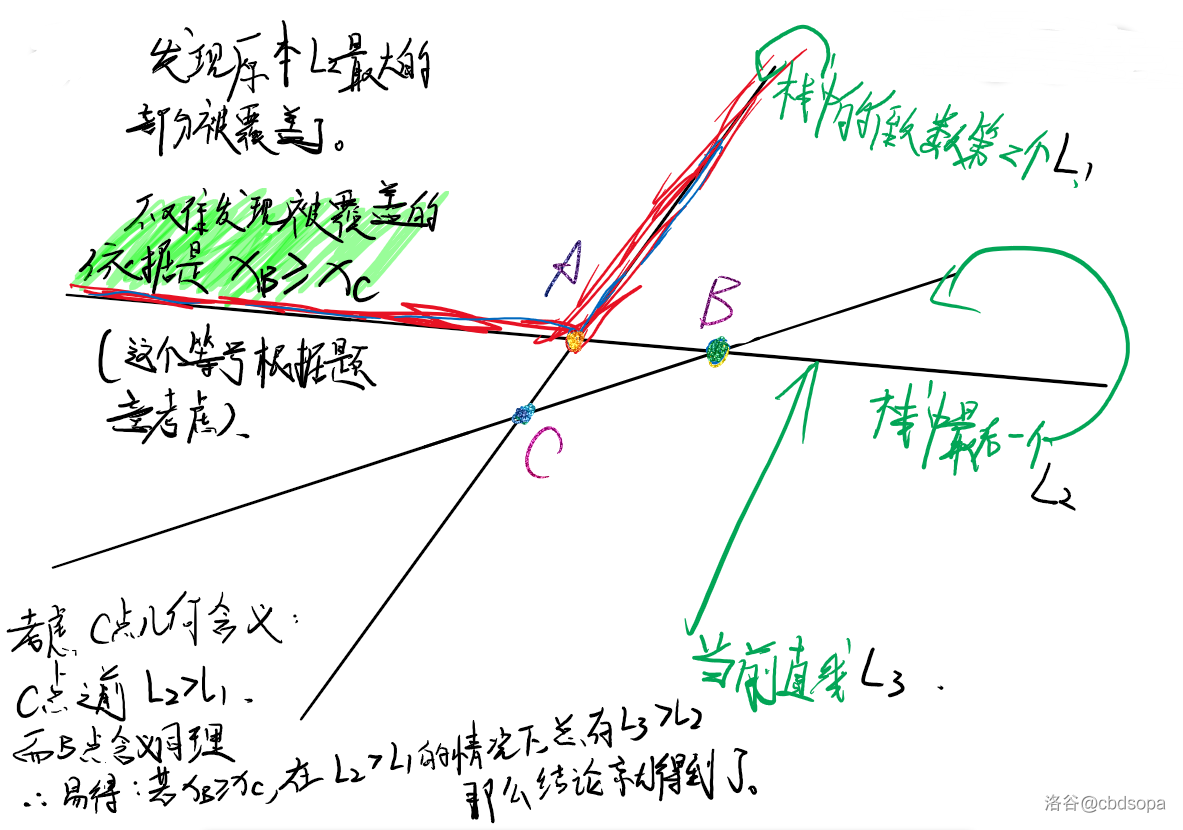
一些简要的证明也在上面了,就不多赘述了。
那么上面理解之后就可以进入下一阶了。
维护凸包
这个区别于凸壳,它维护一堆点的最外圈连线组成的最小凸多边形。
接下来我们提供两种算法。
Graham算法
我们先把y最小的点拿出来,然后以它为中心对其他点极角排序。我们这样做的原因是因为这样y最小的点一定是在凸包里的,思考一下不难发现,因为它不可能与其他点连接形成内凹。
然后我们按照极角排序后的顺序把点一个个加入,一发现出现内凹直接弹掉栈顶。判断是否出现内凹我们用叉积来做,如果当前即将加入的点与栈顶连线在栈中顶上两个点的连线的右侧,可以说明出现内凹。
于是最后得到凸包。
#include<bits/stdc++.h>
#define ll long long
#define db double
#define filein(a) freopen(#a".in","r",stdin)
#define fileot(a) freopen(#a".out","w",stdout)
template<class T>
inline void read(T &s){
s=0;char ch=getchar();bool f=0;
while(ch<'0'||'9'<ch) {if(ch=='-') f=1;ch=getchar();}
while('0'<=ch&&ch<='9') {s=s*10+(ch^48);ch=getchar();}
if(ch=='.'){
int p=10;ch=getchar();
while('0'<=ch&&ch<='9') {s=s+(db)(ch^48)/p;p*=10;;ch=getchar();};
}
s=f?-s:s;
}
const int N=1e5+1;
struct point{
db x,y;
inline friend point operator + (point x,point y){
return (point){x.x+y.x,x.y+y.y};
}
inline friend point operator - (point x,point y){
return (point){x.x-y.x,x.y-y.y};
}
inline friend db operator * (point x,point y){
return x.x*y.y-x.y*y.x;
}
}p[N],st[N];
int n;
inline db dist(point x,point y){
return sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y) );
}
inline bool cmp_ang(point x,point y){
db ax=(x-p[1])*(y-p[1]);
if(ax==0){
return dist(x,p[1])<dist(y,p[1]);
}
return ax>0;
}
int main(){
filein(a);fileot(a);
read(n);
for(int i=1;i<=n;++i){
read(p[i].x);read(p[i].y);
if(i>1 and (p[1].y>p[i].y or (p[1].y==p[i].y and p[1].x>p[i].x)) ){
std::swap(p[1].x,p[i].x);
std::swap(p[1].y,p[i].y);
}
}
std::sort(p+2,p+1+n,cmp_ang);
int top=0;
st[++top]=p[1];
for(int i=2;i<=n;++i){
while(top>1 and (p[i]-st[top])*(st[top]-st[top-1])>=0){
--top;
}
st[++top]=p[i];
}
st[++top]=p[1];
db ans=0;
for(int i=2;i<=top;++i){
ans+=dist(st[i],st[i-1]);
}
printf("%.2lf\n",ans);
return 0;
}
Andrew算法
我们不用极角排序,以x为第一关键字,y为第二关键字排序。这样相对刚才的算法有更加优秀的复杂度。
我们和上面类似的做法,一个个加入,然后弹出右偏的点。
然后就这么弄下去,结果顿时发现不对劲,维护出来的是一个凸壳/jk
所以我们从后往前再推一次,就维护出凸包了。
#include<bits/stdc++.h>
#define ll long long
#define db double
#define filein(a) freopen(#a".in","r",stdin)
#define fileot(a) freopen(#a".out","w",stdout)
template<class T>
inline void read(T &s){
s=0;char ch=getchar();bool f=0;
while(ch<'0'||'9'<ch) {if(ch=='-') f=1;ch=getchar();}
while('0'<=ch&&ch<='9') {s=s*10+(ch^48);ch=getchar();}
if(ch=='.'){
int p=10;ch=getchar();
while('0'<=ch&&ch<='9') {s=s+(db)(ch^48)/p;p*=10;;ch=getchar();};
}
s=f?-s:s;
}
const int N=1e5+1;
int n;
struct point{
db x,y;
inline friend point operator + (point x,point y){
return (point){x.x+y.x,x.y+y.y};
}
inline friend point operator - (point x,point y){
return (point){x.x-y.x,x.y-y.y};
}
inline friend db operator * (point x,point y){
return x.x*y.y-x.y*y.x;
}
};
point p[N],st[N];
inline bool cmp_pos(point x,point y){
if(x.x==y.x){
return x.y<y.y;
}
return x.x<y.x;
}
inline db dist(point x,point y){
return sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y) );
}
int main(){
filein(a);fileot(a);
read(n);
for(int i=1;i<=n;++i){
read(p[i].x);read(p[i].y);
}
std::sort(p+1,p+1+n,cmp_pos);
if(n==1){
printf("0\n");
return 0;
}else if(n==2){
printf("%lf\n",dist(p[1],p[2]) );
return 0;
}
int top=0;
st[++top]=p[1];
st[++top]=p[2];
for(int i=3;i<=n;++i){
while(top>1 and (p[i]-st[top])*(st[top]-st[top-1])>=0) --top;
st[++top]=p[i];
}
int lim=top;
st[++top]=p[n-1];
for(int i=n-2;i>=1;--i){
while(top>lim and (p[i]-st[top])*(st[top]-st[top-1])>=0) --top;
st[++top]=p[i];
}
db ans=0;
for(int i=2;i<=top;++i){
ans+=dist(st[i-1],st[i]);
}
printf("%.2lf\n",ans);
return 0;
}