链式前向星

实际上就是个链表。

#include<bits/stdc++.h>
using namespace std;
int n,m;
vector<bool>vis;
vector<int>head,next,to,val;
/*
head[i]存储以i为起点的第一条边的编号
next[i]存储编号为i的边的同起点的下一条边
to[i]存储编号为i的边所连向的点的编号
val[i]存储编号为i的边的边权
*/
void add(int u,int v,long long w)
{
	next.push_back(head[u]);
	val.push_back(w);
	head[u]=to.size();
	to.push_back(v);
}//加边操作
bool find(int u,int v)
{
	for(int i=head[u];~i;i=next[i]) //~i表示i!=-1
	{
		if(to[i]==v) return 1;
	}
	return 0;
}//查询u到v的边是否存在
void dfs(int x)
{
	if(vis[x]) return;
	vis[x]=1;
	for(int i=head[x];~i;i=next[i]) //~i表示i!=-1
	{
		dfs(to[i]);
	}
}//dfs遍历该图
int main()
{
	scanf("%d%d",&n,&m);//n个点，m条边
	vis.resize(n+1,0);
	head.resize(n+1,-1);
	//初始化
	for(int i=1;i<=m;++i)
	{
		int u,v;
		long long w;
		scanf("%d%d%d",&u,&v,&w);
		add(u,v,w);
		//add(v,u,-w);
	/*上面注释的是存反边，编号为 正边编号^1 ，权值网络流存-w，无
向图存w */
	}
	return 0;
} 

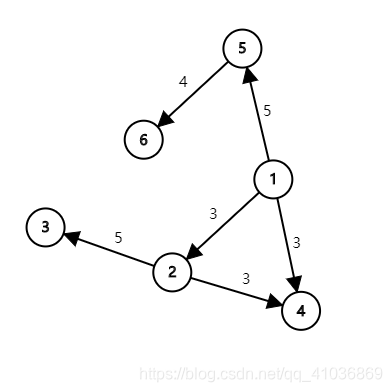
比如要读这个图，就要输入: 6 6 1 2 3 2 4 5 1 3 3 2 3 3 1 5 5 5 6 4 这就不存反边了，这是一个有向图，来模拟一下add过程:

void add(int u,int v,long long w)
{
	next.push_back(head[u]);
	val.push_back(w);
	head[u]=to.size();
	to.push_back(v);
}//加边操作

add(1,2,3): next 0=head 1=-1; val 0=w=3; head 1=0; to 0=v=2;

add(2,4,5): next 1=head 2=-1; val 1=w=5; head 2=1; to 1=v=4;

add(1,3,3): next 2=head 1=0; val 2=w=3; head 1=2; to 2=v=3;

add(2,3,3): next 3=head 2=1; val 3=w=3; head 2=3; to 3=v=3;

add(1,5,5): next 4=head 1=2; val 4=w=5; head 1=4; to 4=v=5;

add(5,6,4): next 5=head 5=-1; val 5=w=4; head 5=5; to 5=v=6;

边连完后的数组情况: next 0=-1; next 1=-1; next 2=0; next 3=1; next 4=2;next 5=-1; val 0=3; val 1=5; val 2=3; val 3=3; val 4=5; val 5=4; head 1=4; head 2=3; head 3=-1; head 4=-1; head 5=5;head 6=-1; to 0=2; to 1=4; to 2=3; to 3=3; to 4=5; to 5=6; 好，这么手推一遍就可以理解这种存储方法的原理了

接下来看查询和遍历； 查询:

bool find(int u,int v)
{
	for(int i=head[u];~i;i=next[i]) //~i表示i!=-1
	{
		if(to[i]==v) return 1;
	}
	return 0;
}//查询u到v的边是否存在

比如我们要查询是否存在边(1,2): find(1,2): 进入了循环: 首先i=head 1=4,然后发现v=2!=to 4=5，i就变成了next 4=2 然后v!=to 2=3,i变成next 2=0 这个时候to 0=2=v 返回存在; 遍历:

void dfs(int x)
{
	if(vis[x]) return;
	vis[x]=1;
	for(int i=head[x];~i;i=next[i]) //~i表示i!=-1
	{
		dfs(to[i]);
	}
}//dfs遍历该图

比如我们从1开始: dfs(1):

x=1进来没走过遍历到1

i=head 1=4,to 4=5没走过遍历到5

i=head 5=5,to 5=6没走过遍历到6

i=head 6=-1,走完了回溯到i=head 5=5

i=next 5=-1,走完了回溯到i=head 1=4

i=next 4=2,to 2=3没走过遍历到3

i=head 3=-1,走完了，回溯到i=next 4=2

i=next 4=2,next 2=0,to 0=2没走过遍历到2

i=head 2=3,to 3=3走过了不管进i=next 3=1;

i=next 3=1,to 1=4没走过,遍历到4,但4里面运行过了回溯回i=next 3=1

i=next 3=1,next 1=-1,走完了进next 4=2再到next 2=3再next 3=1再next 1=-1（中途都走过了）dfs结束

所以遍历顺序为1 5 6 3 2 4