Splay

Splay，即伸展树，较为受众的平衡树，依靠双旋的速度称霸（虽然替罪羊更快，但是splay在之后有光明的未来(可以发展为LCT),总之是比treap快）

平衡树调试两大题:P3369+P6136

注: 本文采用非递归

信息维护

我们对于splay树上的一个节点维护以下信息:

• $sz$ 子树大小
• $fa$ 父节点编号
• $ch[0/1]$ 左右儿子编号(0为左儿子，1为右儿子)
• $val$ 当前点权
• $cnt$ 当前点权的出现次数

以及对与整棵树维护以下信息:

• $tot$ 节点总数
• $rt$ 根节点编号

  基本处理操作

• $update$ 更新当前节点的$sz$
• $stype$ 返回当前节点属于的儿子类型
• $clear$ 销毁当前节点，本质是数组数值清空

	inline void clear(int x){
		t[x].val=t[x].sz=t[x].fa=lc(x)=rc(x)=t[x].val=0;
	}
	inline bool stype(int x){
		return x==rc(fa(x)); 
	} 
	inline void update(int x){
		t[x].sz=t[lc(x)].sz+t[rc(x)].sz+t[x].cnt;
	}

splay维护平衡的操作是旋转，在每次操作后将该节点旋转至根节点保持平衡（实际上就是伸展(splay)操作）

那么先了解旋转(rotate)操作

左旋右旋

本质是把当前节点往上抬

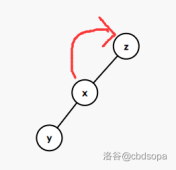
以左旋为例:(对于一个儿子类型为左儿子的节点)具体操作是把要旋转的节点拎起来，然后断掉其右儿子，接到该节点原本的父节点，然后把其原本父节点接到其右子树，再把原本父节点的父节点转为旋转节点的父节点。

我们记旋转节点为 x，其父节点为 y，y 的父节点为 z

其实就是把 x 的右子树腾出来，放置 y，此时 y 左子树的 x 被腾空到y的父节点，所以可以放置 x 需要腾空的右子树，并且把 x 接到原本 y 所在的 z 的儿子位置

然后右旋就是反过来的

如果实在不懂，可以看代码慢慢悟。

	inline void rotate(int x){
		int y=fa(x),z=fa(y);bool ty=stype(x);
		t[y].ch[ty]=t[x].ch[ty^1];
		if(t[x].ch[ty^1]) fa(t[x].ch[ty^1])=y;
		t[x].ch[ty^1]=y;
		fa(y)=x;fa(x)=z;
		if(z) t[z].ch[y==t[z].ch[1]]=x;
		update(y);update(x);
	}

伸展操作(splay)

记伸展节点为 x,其父节点为 y ，y 父节点为 z

我们分为 3 类情况考虑:

1. y直接是splay树的根节点，则对于 x 进行一次旋转
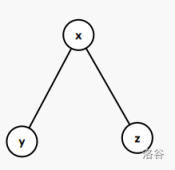
2. 属于”一字型”,则对于 y 旋转，再对于 x 旋转
3. 属于”之字型”,则对于 x 两次旋转即可

什么叫”一字型”,”之字型”?上图！

一字型:

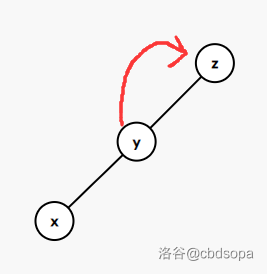
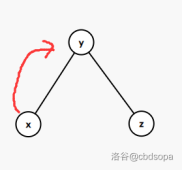
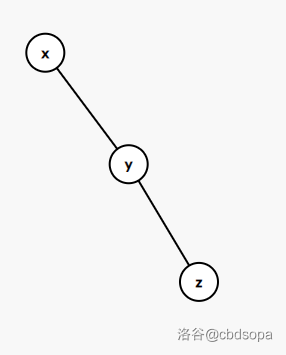
之字型:

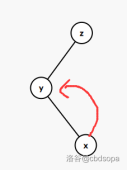
inline void splay(int x){
	for(int f=fa(x);f=fa(x),f;rotate(x))
		if(fa(f))rotate(stype(x)==stype(f)?f:x);
	rt=x;
}

插入操作(ins)

本质是动态开点

如果此时没有建立根节点就直接把值放入根节点，否则向下遍历（小左等中大右），直到找到点权等于该值的，增加计数器，并且更新子树大小，没找到就动态开点，注意要素齐全。最后别忘记把这个点 splay 到根。

	inline void ins(int k)
	{
		if(!rt){
			rt=++tot;
			t[rt].val=k;
			++t[rt].cnt;
			update(rt);
			return;
		}
		int cur=rt,f=0;
		while(1){
			if(t[cur].val==k){
				++t[cur].cnt;
				update(cur);
				update(f);
				splay(cur);
				return;
			}
			f=cur;cur=t[cur].ch[t[cur].val<k];
			if(!cur){
				cur=++tot;
				t[cur].val=k;
				++t[cur].cnt;
				t[cur].fa=f;
				t[f].ch[t[f].val<k]=cur;
				update(cur);
				update(f);
				splay(cur);
				return;
			}
		}
	}

查询数的排名(rk)

遍历，遍历到需要查询的值时返回左边未被选择的数的总数+1。需要特别注意，如果这个值比整个子树都大，会进入空节点，这个时候退出循环并返回左边未被选择总数+1即可。记得伸展。

	inline int rk(int k){
		int cur=rt,res=0;
		while(cur){
			if(k<t[cur].val){
				cur=lc(cur);
			}else{
				res+=t[lc(cur)].sz;
				if(k==t[cur].val){
					splay(cur);
					return res+1;
				}
				res+=t[cur].cnt;
				cur=rc(cur);
			}
		}
		return res+1;
	}

查询此排名的数(kth)

只要注意进右子树寻找时，相当于是在右子树寻找减去左子树和当前点的总sz后的排名。还有为防止左子树为空时进0点，需要特判一下。记得伸展。

	inline int kth(int k){
		int cur=rt;
		while(1){
			if(lc(cur)&&k<=t[lc(cur)].sz){
				cur=lc(cur);
			}else{
				k-=t[cur].cnt+t[lc(cur)].sz;
				if(k<=0){
					splay(cur);
					return t[cur].val;
				}
				cur=rc(cur);
			}
		}
	}

查询前驱后继(pre,nxt)

以前驱为例: 实际上是查询将 x 插入，并 splay 至根后左子树的最大值，进左子树然后一直向右子树跳即可。然后删掉 x （后继同理，反过来的）记得伸展。

	inline int pre(){
		int cur=lc(rt);
		if(!cur) return cur;
		while(rc(cur)) cur=rc(cur);
		splay(cur);
		return cur;
	} 
	inline int nxt(){
		int cur=rc(rt);
		if(!cur) return cur;
		while(lc(cur)) cur=lc(cur);
		splay(cur);
		return cur;
	}

删除操作

先把值对应的点翻到根节点。

分情况:

• 删一个没删完：减计数器并然后更新sz
• 否则:
  • 没有子树：直接删点
  • 只有一个子树：把那一个子树移到根,删点
  • 有两个子树：把左子树最大值移到根，右子树接到根上，删点

唯一一个不需要伸展的操作

	inline void del(int k){
		rk(k);
		if(t[rt].cnt>1){
			--t[rt].cnt;
			update(rt);
			return;
		}
		if(!lc(rt)&&!rc(rt)){
			clear(rt);
        rt=0;
			return;
		}
		if(!lc(rt)){
			int cur=rt;
			rt=rc(rt);
			fa(rt)=0;
			clear(cur);
			return;
		}
		if(!rc(rt)){
			int cur=rt;
			rt=lc(rt);
			fa(rt)=0;
			clear(cur);
			return;
		} 
		int cur=rt,x=pre();
		fa(rc(cur))=x;
		rc(x)=rc(cur);
		clear(cur);
		update(rt);
	}

然后splay就写完了，还挺好理解的。

完整代码

#include<bits/stdc++.h>
using namespace std;
#define file(a) freopen(#a".in","r",stdin),freopen(#a".out","w",stdout)
#define LL long long
#define N 100010
inline int read()
{
	int s=0,f=1;
	char ch=getchar();
	while(ch<'0'||'9'<ch) {if(ch=='-') f=-1;ch=getchar();}
	while('0'<=ch&&ch<='9') {s=s*10+ch-'0';ch=getchar();}
	return s*f;
}
struct Splay{
	#define fa(x) t[x].fa
	#define lc(x) t[x].ch[0]
	#define rc(x) t[x].ch[1]
	int tot,rt;
	struct node{
		int ch[2],fa;
		int sz,cnt,val;
	}t[N];
	Splay(){
		tot=0;rt=0;
	}
	inline void cut_down(){
		tot=0;rt=0;
	}
	inline void clear(int x){
		t[x].val=t[x].sz=t[x].fa=lc(x)=rc(x)=t[x].val=0;
	}
	inline bool stype(int x){
		return x==rc(fa(x)); 
	} 
	inline void update(int x){
		t[x].sz=t[lc(x)].sz+t[rc(x)].sz+t[x].cnt;
	}
	inline void rotate(int x){
		int y=fa(x),z=fa(y);bool ty=stype(x);
		t[y].ch[ty]=t[x].ch[ty^1];
		if(t[x].ch[ty^1]) fa(t[x].ch[ty^1])=y;
		t[x].ch[ty^1]=y;
		fa(y)=x;fa(x)=z;
		if(z) t[z].ch[y==t[z].ch[1]]=x;
		update(y);update(x);
	}
	inline void splay(int x){
		for(int f=fa(x);f=fa(x),f;rotate(x))
			if(fa(f))rotate(stype(x)==stype(f)?f:x);
		rt=x;
	}
	inline void ins(int k)
	{
		if(!rt){
			rt=++tot;
			t[rt].val=k;
			++t[rt].cnt;
			update(rt);
			return;
		}
		int cur=rt,f=0;
		while(1){
			if(t[cur].val==k){
				++t[cur].cnt;
				update(cur);
				update(f);
				splay(cur);
				return;
			}
			f=cur;cur=t[cur].ch[t[cur].val<k];
			if(!cur){
				cur=++tot;
				t[cur].val=k;
				++t[cur].cnt;
				t[cur].fa=f;
				t[f].ch[t[f].val<k]=cur;
				update(cur);
				update(f);
				splay(cur);
				return;
			}
		}
	}
	inline int rk(int k){
		int cur=rt,res=0;
		while(cur){
			if(k<t[cur].val){
				cur=lc(cur);
			}else{
				res+=t[lc(cur)].sz;
				if(k==t[cur].val){
					splay(cur);
					return res+1;
				}
				res+=t[cur].cnt;
				cur=rc(cur);
			}
		}
		return res+1;
	}
	inline int kth(int k){
		int cur=rt;
		while(1){
			if(lc(cur)&&k<=t[lc(cur)].sz){
				cur=lc(cur);
			}else{
				k-=t[cur].cnt+t[lc(cur)].sz;
				if(k<=0){
					splay(cur);
					return t[cur].val;
				}
				cur=rc(cur);
			}
		}
	}
	inline int pre(){
		int cur=lc(rt);
		if(!cur) return cur;
		while(rc(cur)) cur=rc(cur);
		splay(cur);
		return cur;
	} 
	inline int nxt(){
		int cur=rc(rt);
		if(!cur) return cur;
		while(lc(cur)) cur=lc(cur);
		splay(cur);
		return cur;
	}
	inline void del(int k){
		rk(k);
		if(t[rt].cnt>1){
			--t[rt].cnt;
			update(rt);
			return;
		}
		if(!lc(rt)&&!rc(rt)){
			clear(rt);
        rt=0;
			return;
		}
		if(!lc(rt)){
			int cur=rt;
			rt=rc(rt);
			fa(rt)=0;
			clear(cur);
			return;
		}
		if(!rc(rt)){
			int cur=rt;
			rt=lc(rt);
			fa(rt)=0;
			clear(cur);
			return;
		} 
		int cur=rt,x=pre();
		fa(rc(cur))=x;
		rc(x)=rc(cur);
		clear(cur);
		update(rt);
	}
	#undef fa
	#undef rc
	#undef lc
}s; 
int n;
int main(){
	n=read();
	for(int i=1;i<=n;++i){
		int opt=read(),x=read();
		if(opt==1){
			s.ins(x);
		} 
		if(opt==2){
			s.del(x);
		}
		if(opt==3){
			printf("%d\n",s.rk(x));
		}
		if(opt==4){
			printf("%d\n",s.kth(x));
		}
		if(opt==5){
			s.ins(x);
			printf("%d\n",s.t[s.pre()].val);
			s.del(x);
		}
		if(opt==6){
			s.ins(x);
			printf("%d\n",s.t[s.nxt()].val);
			s.del(x);
		}
	}
	return 0;
}

维护区间

其实Splay也是可以维护区间的，思想就是把区间 $[l,r]$ 的端点两边的点 $l-1,r+1$ 分别splay到根和根的右儿子,那么根的右儿子的左儿子就是我们需要操作的区间，下传标记即可。

模板题

更加板子的题

第一个模板题的代码：

#include<bits/stdc++.h>
#define ll long long
#define filein(a) freopen(#a".in","r",stdin)
#define fileot(a) freopen(#a".out","w",stdout)
#define bug(a) printf(#a)
inline int read(){
    int s=0,f=1;char ch=getchar();
    while(ch<'0'||'9'<ch) {if(ch=='-') f=-1;ch=getchar();}
    while('0'<=ch&&ch<='9') {s=s*10+(ch^48);ch=getchar();}
    return s*f;
}
inline int max(int x,int y){
    return x>y?x:y;
}
inline void swap(int &x,int &y){
    int tmp=x;x=y;y=tmp;
}
const int N=5e5+3;
const int inf=0x3f3f3f3f;
const int err=-114514;
int n,m;
int a[N];
int num;
struct Splay{
    #define lc(x) t[x].ch[0]
    #define rc(x) t[x].ch[1]
    #define fa(x) t[x].fa
    int tot,rt;
    int top,bin[N];
    struct node{
        int ch[2],fa;
        int val,cnt,sz;
        int sum,lx,rx,mx;
        bool rev;int vol;
    }t[N];
    inline int newnode(){
        return top?bin[top--]:++tot;
    }
    inline void clear(int x){
        lc(x)=rc(x)=t[x].val=t[x].cnt=t[x].sz=t[x].sum=0;
        fa(x)=t[x].lx=t[x].rx=t[x].mx=t[x].rev=0;
        t[x].vol=err;
        bin[++top]=x;
    }
    inline bool son_type(int x){
        return x==rc(fa(x) );
    }
    inline void update(int x){
        if(!x) return;
		t[x].sum=(t[lc(x)].sum+t[rc(x)].sum+t[x].val);
		t[x].lx=max(t[lc(x)].lx,t[lc(x)].sum+t[rc(x)].lx+t[x].val);
		t[x].rx=max(t[rc(x)].rx,t[rc(x)].sum+t[lc(x)].rx+t[x].val);
		t[x].mx=max(t[lc(x)].rx+t[rc(x)].lx+t[x].val,max(t[lc(x)].mx,t[rc(x)].mx) );
		t[x].sz=(t[lc(x)].sz+t[rc(x)].sz+t[x].cnt);
    }
    inline void pushdown(int x){
		if(t[x].vol!=err){
            if(lc(x) ){
                t[lc(x)].val=t[x].vol;
                t[lc(x)].vol=t[x].vol;
                t[lc(x)].sum=t[x].vol*t[lc(x)].sz;
            }
            if(rc(x) ){
                t[rc(x)].val=t[x].vol;
                t[rc(x)].vol=t[x].vol;
                t[rc(x)].sum=t[x].vol*t[rc(x)].sz;
            }
            if(t[x].vol>=0){
                if(lc(x) ){
                    t[lc(x)].lx=t[lc(x)].rx=t[lc(x)].mx=t[lc(x)].sum;
                }
                if(rc(x) ){
                    t[rc(x)].lx=t[rc(x)].rx=t[rc(x)].mx=t[rc(x)].sum;
                }
            }else{
                if(lc(x) ){
                    t[lc(x)].lx=t[lc(x)].rx=0;
                    t[lc(x)].mx=t[x].vol;
                }
                if(rc(x) ){
                    t[rc(x)].lx=t[rc(x)].rx=0;
                    t[rc(x)].mx=t[x].vol;
                }
            }
			t[x].vol=err;
            t[x].rev=0;
		}else if(t[x].rev){
			if(lc(x) ){
                t[lc(x)].rev^=1;
                swap(lc(lc(x) ),rc(lc(x) ) );
                swap(t[lc(x)].lx,t[lc(x)].rx);
            }
			if(rc(x) ){
                t[rc(x)].rev^=1;
                swap(lc(rc(x) ),rc(rc(x) ) );
                swap(t[rc(x)].lx,t[rc(x)].rx);
            }
            t[x].rev=0;
		}
    }
    inline void rotate(int x){
        int y=fa(x),z=fa(y);bool ty=son_type(x);
        t[y].ch[ty]=t[x].ch[ty^1];
        if(t[x].ch[ty^1]) fa(t[x].ch[ty^1])=y;
        t[x].ch[ty^1]=y;
        fa(x)=z;fa(y)=x;
        if(z) t[z].ch[y==rc(z)]=x;
        update(y);update(x);
    }
    inline void splay(int x,int goal=err){
        if(goal==err) goal=0;
        for(int f=fa(x);(f=fa(x) )!=goal;rotate(x) ){
            if(fa(f)!=goal) rotate(son_type(x)==son_type(f)?f:x);
        }
        if(goal==0) rt=x;
    }
    void del(int cur){
        if(lc(cur) ) del(lc(cur) );
        if(rc(cur) ) del(rc(cur) );
        clear(cur);
    }
	inline int build(int l,int r){
		if(l>r) return 0;
		int mid=(l+r)>>1;
		int pos=newnode();
		t[pos].cnt=1;
		t[pos].val=a[mid];
		t[pos].vol=err;
        t[pos].rev=0;
		if(l==r){
            t[pos].mx=t[pos].sum=a[l];
            t[pos].lx=t[pos].rx=max(a[l],0);
            t[pos].sz=t[pos].cnt=1;
			return pos;
		}
		lc(pos)=build(l,mid-1);
		fa(lc(pos) )=pos;
		rc(pos)=build(mid+1,r);
		fa(rc(pos) )=pos;
		update(pos);
		return pos;
	}
	inline int kth(int k){
		int cur=rt,last=0;
		while(cur){
            pushdown(cur);
			int key=t[lc(cur)].sz+t[cur].cnt;
			if(k<=key){
				if(k<=t[lc(cur)].sz){
					cur=lc(cur);
				}else{
					return cur;
				}
			}else{
				k-=key;
				last=cur;
				cur=rc(cur);
			}
		}
		return last;
	}
	inline int split(int l,int r){
		r+=2;
		l=kth(l);r=kth(r);
        splay(l);splay(r,l);
		return rc(rt);
	}
    inline void opt1(){
        int l=read();
        int tot=read();
        num+=tot;
        for(int i=1;i<=tot;++i){
            a[i]=read();
        }
        int pos1=build(1,tot);
        int pos2=split(l+1,l);
        lc(pos2)=pos1;fa(pos1)=pos2;
        update(pos2);
        update(fa(pos2) );
    }
    inline void opt2(){
        int l=read(),r=read();
        num-=r;r=r+l-1;
        int pos=split(l,r);
        del(lc(pos) );
        lc(pos)=0;
        update(pos);
        update(fa(pos) );
    }
    inline void opt3(){
        int l=read(),r=read(),k=read();
        r=r+l-1;
        int pos=lc(split(l,r) );
        t[pos].vol=k;t[pos].rev=0;
        t[pos].val=k;t[pos].sum=k*t[pos].sz;
        if(k>=0) t[pos].lx=t[pos].rx=t[pos].mx=t[pos].sum;
        else t[pos].lx=t[pos].rx=0,t[pos].mx=k;
        update(fa(pos) );
        update(fa(fa(pos) ) );
    }  
    inline void opt4(){
        int l=read(),r=read();
        r=r+l-1;
        int pos=lc(split(l,r) );
        if(t[pos].vol==err){
            t[pos].rev^=1;
            swap(lc(pos),rc(pos) );
            swap(t[pos].lx,t[pos].rx);
            update(fa(pos) );
            update(fa(fa(pos) ) );
        }
    }
    inline void opt5(){
        int l=read(),r=read();
        r=r+l-1;
        int pos=lc(split(l,r) );
        printf("%d\n",t[pos].sum);
    }
    inline void opt6(){
        printf("%d\n",t[rt].mx);
    }
    #undef lc
    #undef rc
    #undef fa
}s;
int main(){
    //filein(a);fileot(a);
    n=read();m=read();
    a[1]=a[n+2]=s.t[0].mx=-inf;s.t[0].vol=err;
    for(int i=1;i<=n;++i){
        a[i+1]=read();
    }
	s.rt=s.build(1,n+2);
    num=n;
    for(int t=1;t<=m;++t){
        std::string opt;
        std::cin>>opt;
        if(opt=="INSERT"){
            s.opt1();
        }else if(opt=="DELETE"){
            s.opt2();
        }else if(opt=="MAKE-SAME"){
            s.opt3();
        }else if(opt=="REVERSE"){
            s.opt4();
        }else if(opt=="GET-SUM"){
            s.opt5();
        }else if(opt=="MAX-SUM"){
            s.opt6();
        }
        /*
        printf("(%d)[%d]\n",t,num);
        std::cout<<opt<<std::endl;
        printf("    size:%d\n   detail:",num);
        for(int i=1;i<=num;++i){
            int pos=s.t[s.split(i,i) ].ch[0];
            printf("%d ",s.t[pos].val);
        }putchar('\n');
        */
    }
    return 0;
}