最长公共子序列

模板题链接:P2516 HAOI2010最长公共子序列

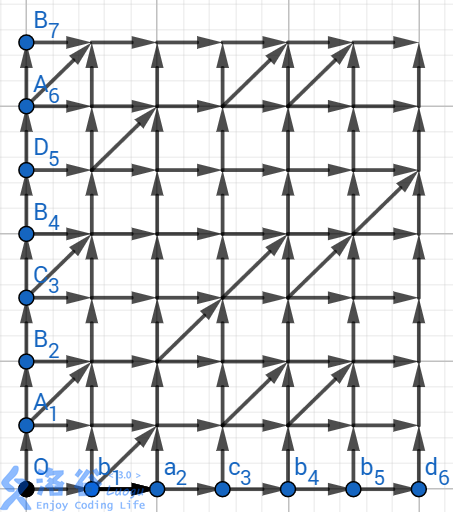
我们借题解第一篇的巨佬的图

我们$O(n^2)$的枚举$i$,$j$(分别对应两个串的下标)

我们记两串分别为$a,b$，记$dp[i][j]$为截止到$i,j$时的最长公共子序列,如果$a[i]==b[j]$匹配成功，我们可直接用$dp[i-1][j-1]+1$来扩展$dp[i][j]$,相当于在网格图中连一条斜边。若没有斜边,我们就通过$dp[i-1][j]$和$dp[i][j-1]$取$max$来扩展。

对于方案的统计，和上面是同理的，只需注意在$dp[i-1][j-1]=dp[i][j]$时，$dp[i][j-1]$和$dp[i-1][j-1]$由$dp[i-1][j-1]$转移来，再分别转移到$dp[i][j]$,是同一种情况，但是被计数了两次，所以要减掉一份。

代码如下：(加了滚动数组)

#include<bits/stdc++.h>
using namespace std;
#define file(a) freopen(#a".in","r",stdin),freopen(#a".out","w",stdout)
#define LL long long
#define N 5010
#define mods (LL)(1e8)
char a[N],b[N];
LL dp[2][N];
LL cnt[2][N];
inline LL Max(LL x,LL y){
	return x>y?x:y;
}
void LCS()
{
	bool now=1,last=0;
	int lena=strlen(a+1),lenb=strlen(b+1);
	//printf("%d %d\n",lena,lenb);
	for(int i=0;i<=lenb;++i) cnt[0][i]=1;
	cnt[1][0]=1;
	for(int i=1;i<=lena;++i,now^=1,last^=1)
	{
		for(int j=1;j<=lenb;++j)
		{
			cnt[now][j]=0;
			dp[now][j]=((a[i]==b[j])?dp[last][j-1]+1:Max(dp[last][j],dp[now][j-1]));
			if(a[i]==b[j]){
				cnt[now][j]+=cnt[last][j-1];
			}
			if(dp[now][j]==dp[now][j-1]){
				cnt[now][j]+=cnt[now][j-1];
			}
			if(dp[now][j]==dp[last][j]){
				cnt[now][j]+=cnt[last][j];
			}
			if(dp[now][j]==dp[last][j-1]){
				cnt[now][j]-=cnt[last][j-1];
			}
			cnt[now][j]%=mods;
		}
	}
	printf("%lld\n%lld",dp[last][lenb],cnt[last][lenb]);
}
int main(){
	int top=0;
	char ch=getchar();
	while(ch!='.') {a[++top]=ch;ch=getchar();}
	//cout<<top<<endl;
	ch=getchar();
	top=0;ch=getchar();
	while(ch!='.') {b[++top]=ch;ch=getchar();}
	//cout<<top<<endl;
	LCS();
	return 0;
}